Multiple Linear Regression using Tensorflow Optimization
Want to share your content on python-bloggers? click here.
This post implements the optimization based estimation of multiple linear regression model using Tensorflow. With this example, we can learn basic implementations of functions in Python and a numerical optimization in Tensorflow.
Optimization based Linear Regression using Tensorflow
This post deals with an optimization based linear regression model using Python and Tensorflow to learn some basic functionalities in them. This regression also can be easily estimated by using the standard matrix formula as in the previous post.
Minimization of Residual Sum of Squares
Multiple linear regression model has the following expression. \((t=1,2,…,n)\)
\[\begin{align} Y_t&=\beta_0+\beta_1 X_{1t}+⋯+\beta_{p-1} X_{p-1,t}+\epsilon_t \end{align}\]
To estimate the regression coefficients \(\beta\), we minimize the sum of squared residuals directly by using numerical optimization in Tensorflow.
\[\begin{align} \min_{\beta} \sum_{t=1}^{n} (Y_t – \beta_0-\beta_1 X_{1t}-⋯-\beta_{p-1} X_{p-1,t})^2 \end{align}\]
Python code using Tensorflow
To use a numerical optimization such as Nelder-Mead algorithm, we need to import tensorflow_probability package.
import tensorflow_probability as tfp | cs |
To use a numerical optimization, we also define an objective function using def command in Python, which returns a residual sum of squares. In fact we define two objective functions : objfunc_w_args(beta, y, X) and objfunc_wo_args(beta). The former is with another arguments except a vector of parameters (beta) but the latter is without another arguments. Therefore from these two types of objective functions, there are some modifications when we call a numerical optimization function in Tensorflow (tfp.optimizer.nelder_mead_minimize).
# -*- coding: utf-8 -*- “”“ #========================================================# # Quantitative ALM, Financial Econometrics & Derivatives # ML/DL using R, Python, Tensorflow by Sang-Heon Lee # # https://kiandlee.blogspot.com #——————————————————–# # Linear Regression model using Tensorflow Optimization #========================================================# ““” import numpy as np from sklearn import datasets, linear_model import tensorflow as tf import tensorflow_probability as tfp # optimizer “”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“ Load the diabetes dataset ““”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“” X, y = datasets.load_diabetes(return_X_y=True) nr, nc = X.shape; print (nr, nc) nparam = nc+1 # number of parameters v_row_name = np.hstack( [[“const”], [“X”+str(i) for i in range(1,nc+1)]]) # regression estimation using sklearn mod = linear_model.LinearRegression() # object mod.fit(X, y) # estimation or tradining param = np.hstack([mod.intercept_, mod.coef_]) “”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“ Objective Function : RSS ““”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“” # with another arguments such as data def objfunc_w_args(beta, y, X): n = len(beta) mbeta = tf.reshape(tf.cast(beta,tf.float64),[n,1]) err = y – tf.matmul(X, mbeta) # element-wise product RSS = tf.reduce_sum(tf.math.multiply(err, err)) return RSS # without any arguments except a vector of parameters def objfunc_wo_args(beta): n = len(beta) mbeta = tf.reshape(tf.cast(beta,tf.float64),[n,1]) err = my – tf.matmul(m1X, mbeta) return tf.reduce_sum(err ** 2) “”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“ Data Preparation for Tensorflow ““”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“” my = tf.constant(y, shape=[nr, 1]) mX = tf.constant(X, shape=[nr, nc]) m1 = tf.cast(tf.ones([nr, 1]), tf.float64) m1X = tf.concat([m1, mX], 1); # 1, X “”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“ Optimization ““”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“”“” # initial guess for parameters start = tf.constant([1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.], dtype=tf.float64) print(“\n========== w/o arguments ==========”) optim_results_wo = tfp.optimizer.nelder_mead_minimize( objfunc_wo_args, initial_vertex=start, func_tolerance=1e–15, position_tolerance=1e–15) print(optim_results_wo.position) print(optim_results_wo.converged) print(“\n========== with arguments ==========”) optim_results_w = tfp.optimizer.nelder_mead_minimize( lambda beta: objfunc_w_args(beta, my, m1X), initial_vertex=start, func_tolerance=1e–15, position_tolerance=1e–15) print(optim_results_w.position) print(optim_results_w.converged) print(“\n========== sklearn ==========”) print(param) | cs |
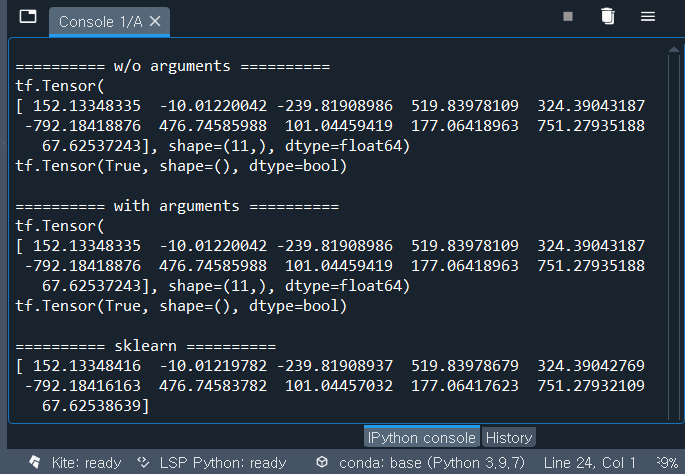
As can be seen in the output below, results from the numerical optimization is nearly the same as the result from sklearn package which is based on matrix formula since there are negligible numerical errors.
Concluding Remarks
This post dealt with how to define functions and run optimizations in Tensorflow. Now that we have learn some basic how-to regarding Tensorflow, a state space model with Kalman filtering and estimation of parameter with numerical optimization will be discussed in the next post. \(\blacksquare\)
Want to share your content on python-bloggers? click here.